Algoritmo de Ordenamiento de Burbuja (Bubble Sort)

El algoritmo de ordenamiento de burbuja (Bubble Sort) es un algoritmo sencillo de ordenamiento que busca mediante repetidas comparaciones de los elementos adyacentes ordenar un conjunto de elementos. Actualmente existen diferentes algoritmos de ordenamiento mucho más óptimos que este, por lo cual se utiliza más que todo como herramienta de educación en lógica y algoritmia.
Algoritmo paso a paso
Supongamos que tenemos un conjunto de elementos sin ordenar como el siguiente:

Los subíndices P1 a P5 indican la posición de cada elemento en el arreglo. Como son cinco posiciones se realizarán cuatro verificaciones entre los elementos adyacentes así:
Si P1 > P2 se intercambian
Si P2 > P3 se intercambian
Si P3 > P4 se intercambian
Si P4 > P5 se intercambianCon esto podemos asegurar que el último elemento de la colección está ordenado. Lo que sigue, son subsecuentes iteraciones del mismo procedimiento excluyendo el último elemento cada vez. Empecemos.
En esta iteración se verifica P1 > P2, como 30 > 20 se intercambian y queda [20,30,10,5,0].

En esta iteración se verifica P2 > P3, como 30 > 10 se intercambian y queda [20,10,30,5,0].
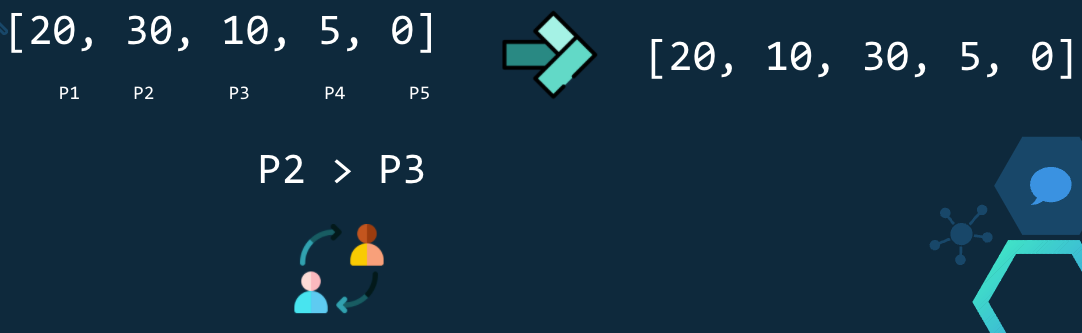
En esta iteración se verifica P3 > P4, como 30 > 5 se intercambian y queda [20,10,5,30,0].
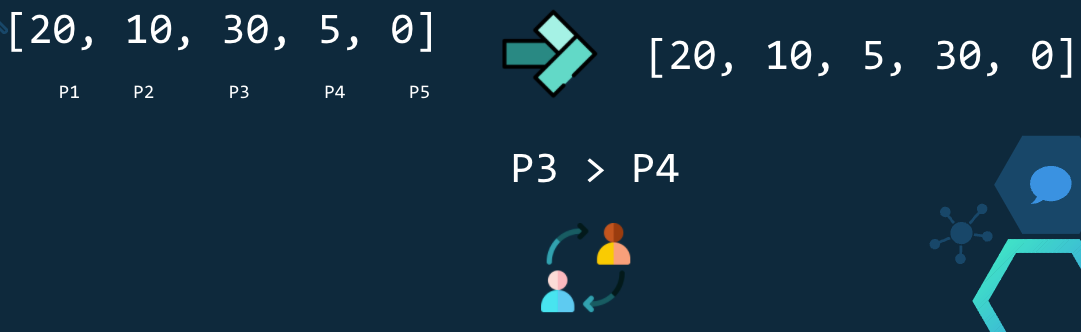
En esta iteración se verifica P4 > P5, como 30 > 0 se intercambian y queda [20,10,5,0,30].
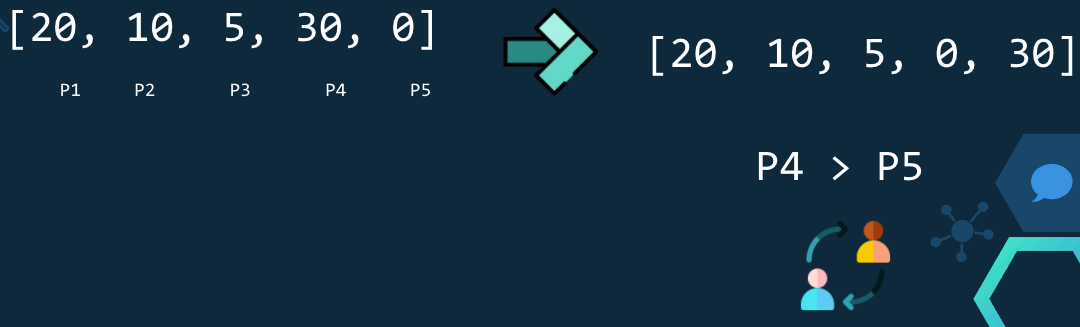
Como puedes darte cuenta en este punto una vez terminada nuestra primera ronda de iteraciones podemos asegurar que el elemento del final está ordenado. Dado que el número 30 estaba en la primera posición, en cierta forma, este algoritmo "hala" los elementos de izquierda a derecha.
La siguiente iteración que vamos a aplicar sería la siguiente:
Si P1 > P2 se intercambian
Si P2 > P3 se intercambian
Si P3 > P4 se intercambianEn esta iteración se verifica P1 > P2, como 20 > 10 se intercambian y queda [10,20,5,0,30].

En esta iteración se verifica P2 > P3, como 20 > 5 se intercambian y queda [10,5,20,0,30].
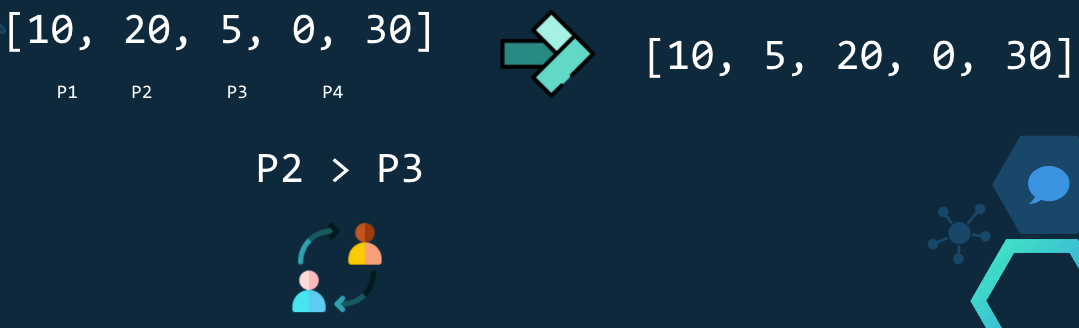
En esta iteración se verifica P3 > P4, como 20 > 0 se intercambian y queda [10,5,0,20,30].
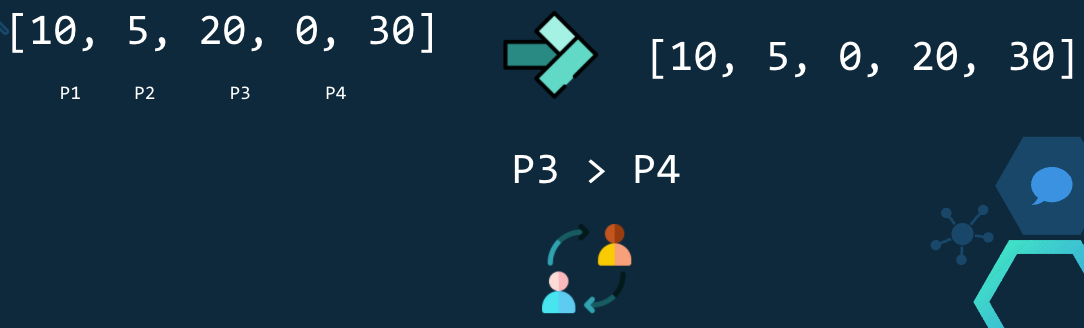
En este punto ya es clara la siguiente serie de comprobaciones.
Si P1 > P2 se intercambian
Si P2 > P3 se intercambianEn esta iteración se verifica P1 > P2, como 10 > 5 se intercambian y queda [5,10,0,20,30].
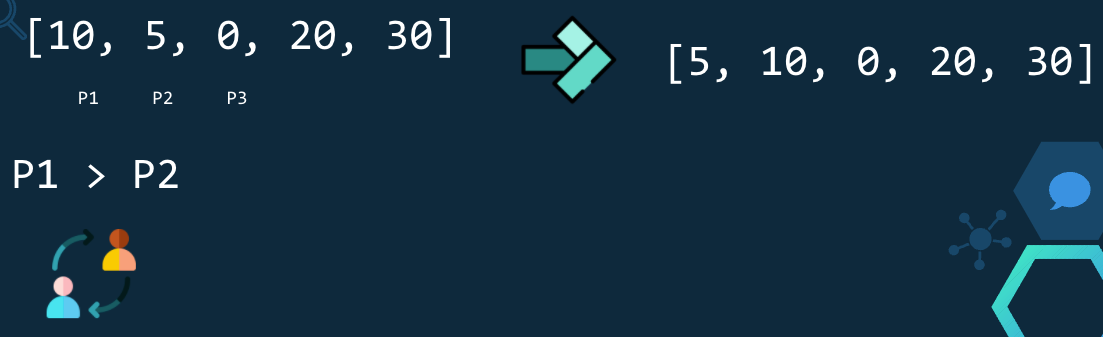
En esta iteración se verifica P2 > P3, como 10 > 0 se intercambian y queda [5,0,10,20,30].
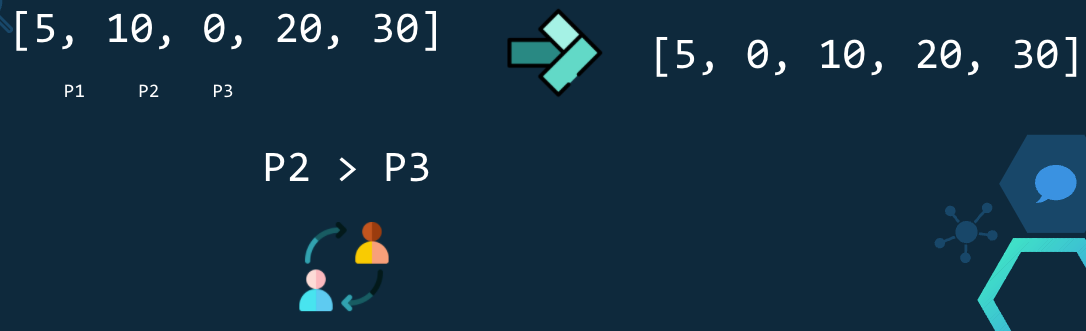
La última iteración que realizaremos será la siguiente:
Si P1 > P2 se intercambianEn esta iteración se verifica P1 > P2, como 5 > 0 se intercambian y queda [0,5,10,20,30].

Como ves finalmente el arreglo de elementos queda ordenado.
Pseudocódigo
El pseudocódigo para este algoritmo es el siguiente:
procedure bubbleSort(A : collection)
n := length(A)
for i := 1 to n-1 inclusive do
for j := 1 to n-i inclusive do
if A[j-1] > A[j] then
swap(A[j-1], A[j])
end if
end for
end for
end procedureOptimización
Si te das cuenta este algoritmo no está optimizado. Supongamos que recibimos una colección de elementos que ya está ordenada, aún así este algoritmo realizaría todas las iteraciones solo para devolver la misma colección sin alterarla.
Para solventar esto es necesario al menos hacer una iteración sobre los elementos, y en caso de no realizarse ningún intercambio de posiciones supondremos que la colección ya está ordenada. Con esto el pseudocódigo quedaría así:
procedure bubbleSort(A : collection)
n := length(A)
for i := 1 to n-1 inclusive do
swapped := false
for j := 1 to n-i inclusive do
if A[j-1] > A[j] then
swapped := true
swap(A[j-1], A[j])
end if
end for
if not swapped
break
end if
end for
end procedurePuedes ver una implementación de este algoritmo en PHP el siguiente post.
Implementación del algoritmo Bubble Sort (ordenamiento de burbuja) en PHP