Criptografía asimétrica en OpenSSL - Llave pública

En nuestro post anterior vimos lo básico para comenzar con openssl y sus algoritmos de encriptación. El día de hoy iremos un poco más allá y veremos la criptogtafía asimétrica o criptografía de dos llaves.
Definición
La criptografía asimétrica o de dos llaves, como su nombre lo indica, es un sistema criptográfico que utiliza dos llaves para el envío y recepción de mensajes. Estas dos llaves pertenecen a una misma persona y una de ellas es pública y la otra privada. Esta persona debe asegurar que su llave privada jamás llegue a manos de otra persona. Por el contrario su llave pública debe ser compartida con otros usuarios para permitir el envío o recepción de mensajes. La criptografía asimétrica asegura dos atributos de la información, la confidencialidad (cifrado con llave pública) y la autenticidad (cifrado con llave privada).
En este post nos centraremos en tratar la confidencialidad. Es decir, que un mensaje enviado no pueda ser descrifrado más que por la persona a la cuál va dirigido. Veamos el siguiente ejemplo.
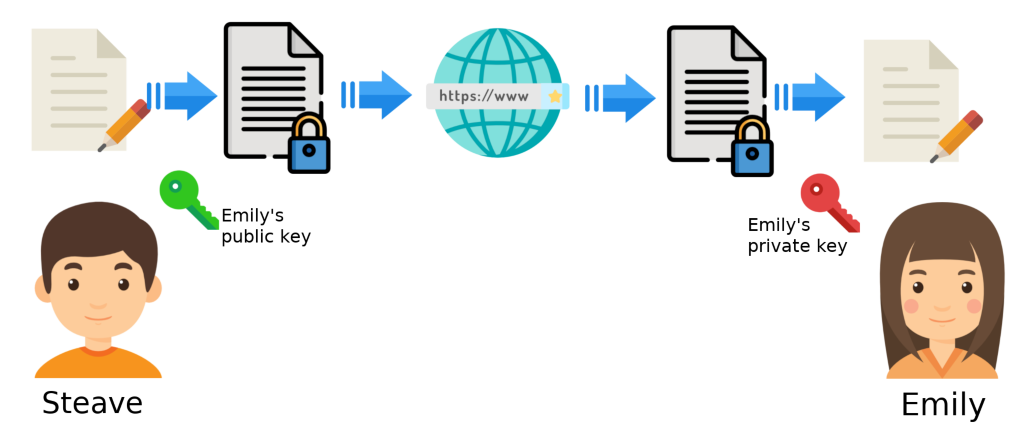
Supongamos que Steave desea enviarle un mensaje de manera confidencial a Emily. Porsupuesto ambos eligieron la criptografía asimétrica para tal fin. Para que este esenario sea posible únicamente se necesitan las dos llaves (pública y privada) de Emily. A continuación se enumera la serie de pasos para el envío y recepción del mensaje en mención.
- Steave escribe el mensaje que le enviará a Emily.
- Steave encripta con la llave pública de Emily el mensaje que le enviará.
- Steave envía el mensaje a través de internet.
- Emily recibe el mensaje encriptado de Steave.
- Emily utiliza su llave privada para descifrar el mensaje y poder leerlo.
Como puedes ver, este esquema simple de envío de información implica que los mensajes en primer lugar son cifrados antes de ser enviados a través de un canal como internet (sí es bastante obvio). En segundo lugar, la persona receptora del mensaje debe compartir su llave pública para que con ella sean crifrados los mensajes que se le enviarán. Estos mensajes cifrados no pueden ser descifrados más que por su receptor, ni siquiera la persona remitente puede descifrarlo una vez cifrado. En tercer lugar, se presume que la persona a la cuál va dirigido el mensaje es la única que tiene la llave privada que descifrará el mensaje, con lo cual, podemos decir que se asegura la confidencialidad del mensaje.
Una de las mejores analogías que he encotrado para entender esto con un ejemplo de la vida real es el de la ranura del buzón o correo. Podemos suponer, que la ranura de nuestro buzón es la llave pública, puesto que está expuesta y cualquier persona que sepa su ubicación (nuestra dirección) estaría en capacidad de enviarnos un mensaje allí. Por otro lado, sólo la persona que posee la llave del buzón puede abrir los mensajes allí contenidos, en esencia, solo nosotros poseemos la llave, por lo tanto son confidenciales. Esto se asimila mucho a la criptografía asimétrica, observa que incluso, una persona que nos haya escrito un mensaje y lo haya introducido en la ranura (cifrado) no podrá volver a verlo (descrifrarlo).
Generación de las llaves
Para generar una llave privada basta ejecutar el siguiente comando:
openssl genrsa -out key.pem 1024El producto de la ejecución de este comando es el archivo key.pem y su contenido será similar al que se muestra a continuación
-----BEGIN RSA PRIVATE KEY-----
MIICXAIBAAKBgQC/p+SkOM3pAPvauL+HvOj9R7ME4Mauy5Vr661fQg2nmMqsyPKM
cRJzod+qEJPiGrNPpPxZUq0OOaW1oLJF+s5hbh46peQb86Yh4TDZZsy0gpFov6KA
LrsHseTnZH+dayLkgMEof6ddVWjWS+p1J9hx8D1Efm55pZyIVWHz1UGr/wIDAQAB
AoGAffQawQpL2Hs7CU0tIkm2XO4H6obGTA2jT199ewLv8lrpp5AQRtfwpmmVkjB+
37NocEkfRpyc+qJMEwde4bqoch4H71Q/gzRC9Kkph8814A+XjnD3lwrL0sSYdi4k
UGz1nPKudT5ls3CkJFs+rx0/CThAB6E3+qezLt8+1TWmSXECQQD6wCEUsIU8NaVf
HDOO76H/C6jdc3+eQSVR40kyYMOscWe0NzzB3KQnnpJIYLZvkHRUytSdBgNz8dNo
mcp0LUNFAkEAw6sNYZxAKgLposU+nlplX6jmq3PqKnCB7aDP+kHzi5ypMo/XYno4
qOORiWL0G4q/sFaJmQ/yeyUrbhvuV6fkcwJBAPARbFqbmiQIFHkXzgEGSmmdpyHG
B6PjKTDaU2UJIa4CsU/oJqJQdVV9Sv5Cocf0XHwl6SMg88NY/pfBzgQmpaUCQA4z
20vLgKjL/1NuR8ZMv3D7HIszZbrg4b1y38XFhb0LiQh/gl3Gi1hO9GBpi1h4cMOG
9IPksXAY2Zcrddhs+lsCQAHvd+q17h9ofpwsvx6RrEIzCJD9tbwPdKWdqkJOSJgc
jPzZIDA4bpPNCFZzZq3IYR2rEK800lxrVgNKtKWRkVQ=
-----END RSA PRIVATE KEY-----
Es importante que te vayas familiarizando con cada uno de los resultados que puede arrojar un comando en openssl para reconocer las llaves privadas, públicas, certificados, entre otros.
Por defecto la llave es creada en formato PEM. Para elegir entre cualquiera de los formatos DER o NET debes utilizar la opción -outform para convertir el PEM al formato elegido.
openssl genrsa -in key.pem -outform DER -out key.der 1024De la llave privada se extrae la parte que será la llave pública. Para hacer esto ejecutamos el siguiente comando:
openssl rsa -in key.pem -pubout -out pub-key.pemEl producto de la ejecución de este comando es el archivo pub-key.pem y su contenido será similar al que se muestra a continuación
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQC/p+SkOM3pAPvauL+HvOj9R7ME
4Mauy5Vr661fQg2nmMqsyPKMcRJzod+qEJPiGrNPpPxZUq0OOaW1oLJF+s5hbh46
peQb86Yh4TDZZsy0gpFov6KALrsHseTnZH+dayLkgMEof6ddVWjWS+p1J9hx8D1E
fm55pZyIVWHz1UGr/wIDAQAB
-----END PUBLIC KEY-----
Ya tenemos nuestra llave pública (pub-key.pem) y privada (key.pem). Vamos a ver ahora como enviar un mensaje encriptado siguiendo el esquema planteado anteriormente.
Encriptación
Supongamos que queremos enviar un mensaje y tenemos la llave pública de la persona remitente que en nuestro caso es pub-key.pem. Para encriptar un mensaje con esta llave pública debemos utilizar el comando openssl rsautl con la opción -encrypt.
echo "Hola mundo" > message.txt
openssl rsautl -encrypt -inkey pub-key.pem -pubin -in message.txt -out message.enc
El producto de esta ejecución es el archivo message.enc el cuál podemos enviar al destinatario. Por consiguiente, dicho destinatario podrá desencriptar el mensaje básicamente con el mismo comando con la opción -decrypt.
openssl rsautl -decrypt -inkey key.pem -in message.enc -out message.decEl contenido del archivo message.dec contendrá el mensaje original.