Asymmetric Cryptography in OpenSSL - Public Key

In our previous post, we saw the basics to get started with OpenSSL and its encryption algorithms. Today, we will go a little further and explore asymmetric cryptography or two-key cryptography.
Definition
Asymmetric cryptography or two-key cryptography, as its name indicates, is a cryptographic system that uses two keys for the sending and receiving of messages. These two keys belong to the same person, and one of them is public, while the other is private. This person must ensure that their private key never falls into the hands of another person. On the contrary, their public key must be shared with other users to allow the sending or receiving of messages. Asymmetric cryptography ensures two attributes of the information: confidentiality (encrypted with the public key) and authenticity (encrypted with the private key).
In this post, we will focus on addressing confidentiality. That is, a message sent can only be decrypted by the person to whom it is directed. Let's see the following example.
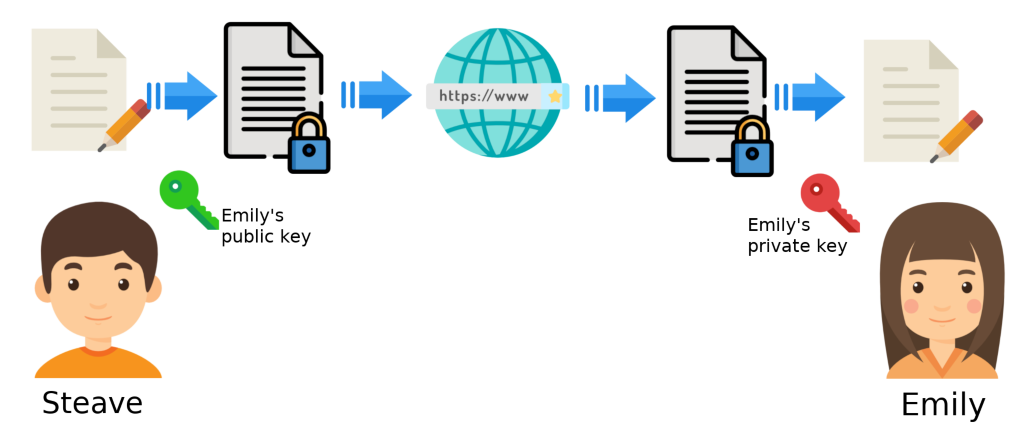
Let's suppose that Steve wants to send a confidential message to Emily. Of course, both have chosen asymmetric cryptography for this purpose. For this scenario to be possible, only Emily's two keys (public and private) are needed. The following are the steps for sending and receiving the mentioned message.
- Steve writes the message he will send to Emily.
- Steve encrypts the message he will send with Emily's public key.
- Steve sends the message over the internet.
- Emily receives the encrypted message from Steve.
- Emily uses her private key to decrypt the message and read it.
As you can see, this simple information sending scheme implies that messages are first encrypted before being sent through a channel like the internet (yes, it is quite obvious). Secondly, the message recipient must share their public key so that the messages sent to them can be encrypted with it. These encrypted messages can only be decrypted by their intended recipient; not even the sender can decrypt them once they are encrypted. Thirdly, it is presumed that the person to whom the message is directed is the only one who has the private key that will decrypt the message, ensuring the confidentiality of the message.
One of the best analogies I have found to understand this with a real-life example is the mailbox or mail slot. We can assume that the mailbox slot is the public key since it is exposed, and anyone who knows its location (our address) would be able to send us a message there. On the other hand, only the person who has the key to the mailbox can open the messages inside it. Essentially, only we possess the key, and therefore, the messages are confidential. This is very similar to asymmetric cryptography. Notice that even a person who has written us a message and inserted it in the slot (encrypted) will not be able to see it again (decrypt it).
Key Generation
To generate a private key, simply execute the following command:
-----BEGIN RSA PRIVATE KEY-----
MIICXAIBAAKBgQC/p+SkOM3pAPvauL+HvOj9R7ME4Mauy5Vr661fQg2nmMqsyPKM
cRJzod+qEJPiGrNPpPxZUq0OOaW1oLJF+s5hbh46peQb86Yh4TDZZsy0gpFov6KA
LrsHseTnZH+dayLkgMEof6ddVWjWS+p1J9hx8D1Efm55pZyIVWHz1UGr/wIDAQAB
AoGAffQawQpL2Hs7CU0tIkm2XO4H6obGTA2jT199ewLv8lrpp5AQRtfwpmmVkjB+
37NocEkfRpyc+qJMEwde4bqoch4H71Q/gzRC9Kkph8814A+XjnD3lwrL0sSYdi4k
UGz1nPKudT5ls3CkJFs+rx0/CThAB6E3+qezLt8+1TWmSXECQQD6wCEUsIU8NaVf
HDOO76H/C6jdc3+eQSVR40kyYMOscWe0NzzB3KQnnpJIYLZvkHRUytSdBgNz8dNo
mcp0LUNFAkEAw6sNYZxAKgLposU+nlplX6jmq3PqKnCB7aDP+kHzi5ypMo/XYno4
qOORiWL0G4q/sFaJmQ/yeyUrbhvuV6fkcwJBAPARbFqbmiQIFHkXzgEGSmmdpyHG
B6PjKTDaU2UJIa4CsU/oJqJQdVV9Sv5Cocf0XHwl6SMg88NY/pfBzgQmpaUCQA4z
20vLgKjL/1NuR8ZMv3D7HIszZbrg4b1y38XFhb0LiQh/gl3Gi1hO9GBpi1h4cMOG
9IPksXAY2Zcrddhs+lsCQAHvd+q17h9ofpwsvx6RrEIzCJD9tbwPdKWdqkJOSJgc
jPzZIDA4bpPNCFZzZq3IYR2rEK800lxrVgNKtKWRkVQ=
-----END RSA PRIVATE KEY-----
It is important to familiarize yourself with each of the results that can be obtained from an openssl command to recognize private keys, public keys, certificates, among others.
By default, the key is created in PEM format. To choose between any of the DER or NET formats, you must use the -outform option to convert the PEM to the chosen format.
openssl genrsa -in key.pem -outform DER -out key.der 1024From the private key, we extract the part that will be the public key. To do this, we execute the following command:
openssl rsa -in key.pem -pubout -out pub-key.pemThe result of executing this command is the file pub-key.pem and its contents will be similar to the following:
-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQC/p+SkOM3pAPvauL+HvOj9R7ME
4Mauy5Vr661fQg2nmMqsyPKMcRJzod+qEJPiGrNPpPxZUq0OOaW1oLJF+s5hbh46
peQb86Yh4TDZZsy0gpFov6KALrsHseTnZH+dayLkgMEof6ddVWjWS+p1J9hx8D1E
fm55pZyIVWHz1UGr/wIDAQAB
-----END PUBLIC KEY-----
We now have our public key (pub-key.pem) and private key (key.pem). Let's see now how to send an encrypted message following the previously discussed scheme.
Encryption
Let's assume that we want to send a message and we have the public key of the sender, which in our case is pub-key.pem. To encrypt a message with this public key, we must use the openssl rsautl command with the -encrypt option.
echo "Hello world" > message.txt
openssl rsautl -encrypt -inkey pub-key.pem -pubin -in message.txt -out message.enc
The result of this execution is the file message.enc, which can be sent to the recipient. Consequently, the recipient can decrypt the message using basically the same command with the -decrypt option.
openssl rsautl -decrypt -inkey key.pem -in message.enc -out message.decThe contents of the file message.dec will contain the original message.